今回は、「生物基礎」の予備学習に登場するミクロメーターの計算問題の解き方を紹介します。演習問題をわかりやすく解説しているので、わからない人でも図の見方や計算に挑戦してみましょう。
※2020年4月中旬頃に、問題をつくり直しました。前回と内容が一部異なります。
演習問題
下のスライドは典型的なミクロメーターの計算問題です。まずは問題を見てチャレンジしてみましょう。10分悩んで全く手が出ない場合は、すぐに解説を見ましょう。
修正:問6の『速度』を『速さ』に変更、2020/4/26。
チャレンジしてみてどうだったでしょうか。以下の解答・解説を確認して、復習してみてください。
解答
解答は、次の通りです。
問1.10μm
問2.4.2μm(4.16…μmを四捨五入)
問3.長さは小さくなる。(9文字)
問4.75μm
問5.原形質流動
問6.5μm/秒(今回は有効数字の指定なし)
解説
問1.対物ミクロメーターの1目盛りの長さは暗記!
対物ミクロメーターの1目盛りの長さは何μmか、答えなさい。ただし、対物ミクロメーター1目盛りは、1mmを百分の一にした値である。
この問題は知識or計算問題です。対物ミクロメーターの長さを答える問題でした。
対物ミクロメーターは、その1目盛りが10μmになるように作られています。よって、暗記するように習った方は、即答できたと思います。また、暗記できていなかった方のために、1目盛りが1mmの百分の一であるというヒントを出し、10μmと計算で導けるようにしておきました。
今回の出題のようにヒントがある場合もありますが、多くの問題ではヒントがありません。なので、対物ミクロメーターの長さが10μmであることは、暗記しておいた方がよいです。
問2.公式を使って計算しよう!
図1から、この倍率における接眼ミクロメーター1目盛りの長さは何μmか。割りきれない場合は、小数点第二位を四捨五入しなさい。
この問題は図の読み取りと計算問題です。接眼ミクロメーター1目盛りの長さを求める、典型計算問題でした。
接眼ミクロメーター1目盛りの長さを求めるためには、
- 接眼ミクロメーターと対物ミクロメーターの一致目盛り数を確認する。(図の読み取り)
- ミクロメーターの公式に当てはめる。(計算)
という手順を踏みます。
まず、接眼ミクロメーターと対物ミクロメーターを照らし合わせて、目盛りが重なったところを探しましょう。この問題では、下のスライド2で示したところが、目盛りが重なっているところです。
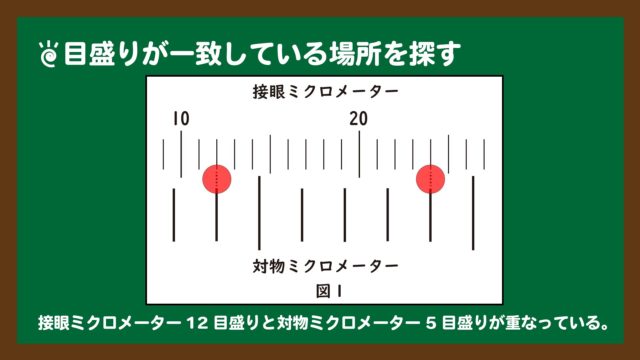 スライド2:目盛りの一致を探す
スライド2:目盛りの一致を探す目盛りが一致する場所は、必ず最低2か所あります。必ず完全に一致している場所を見つけましょう。また、一見一致しているように見えても重なっていない場所はあるので、そこを選ばないように注意深く読み取る必要があります。
次に、公式を使って計算します。公式の詳細とこの問題で公式を使った場合は、以下のスライド3のようになります。
 スライド3:ミクロメーターの公式を使う
スライド3:ミクロメーターの公式を使う割りきれないときは小数点第二位を四捨五入するとあったので、それに従います。問題によっては割り切れるときもあれば、有効数字の指定があることもあります。
ちなみに、実際の定期テストや入試問題では、公式がヒントとして書いてあることはありません。公式は必ず暗記しておきましょう。ちなみに管理人は、「たい(上)せつ(下)な10μm(掛け算)」というように覚えています。
公式の作り方について、スクロール下方で紹介しています。簡単に理解できるので読んでみてください。
接眼ミクロメーターには目盛りがありますが、その目盛りの長さは倍率によって変化するので定まっていません。なので、接眼ミクロメーターの1目盛りの長さを求めるときは、必ず対物ミクロメーターと照らし合わせて計算する必要があります。
問3.倍率の変化に伴う視野の広さの変化は頻出!
対物レンズの倍率を4倍に大きくした場合、接眼ミクロメーター1目盛りの長さはどうなるか。10文字以内で記述しなさい。
この問題は考察問題です。倍率が大きくなったときの接眼ミクロメーター1目盛りの長さの変化を答える問題でした。
考察のヒントとしては、倍率が大きくなることで視野の広さがどう変わるかを考えることが挙げられます。そのことについて、解説します。
まず、倍率が変わったときの接眼ミクロメーターの見え方を理解しましょう。これは経験しないとわからないことですが、倍率が変化しても、顕微鏡で見える接眼ミクロメーターの目盛りの見え方に変化はないです。例を挙げると、下のスライド4のようになります。
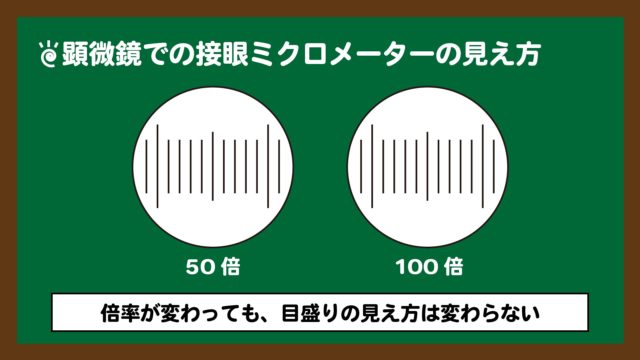 スライド4:倍率が変わっても接眼ミクロメーターの見え方は変わらない。
スライド4:倍率が変わっても接眼ミクロメーターの見え方は変わらない。どちらの倍率でも、視野の目盛り数が同じだとわかるはずです。
ただし、倍率が変わると、見えている視野の広さは変わります。対物レンズの倍率が4倍になると、見える視野の一辺は4分の1になり、見える視野の広さは16分の1になります。図で表すと、下のスライド5のようになります。
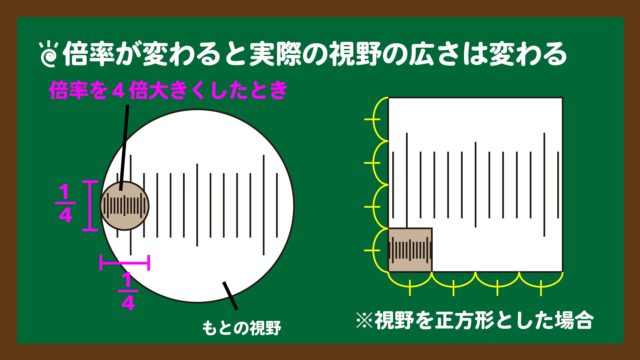 スライド5:倍率が変わると実際の視野の広さは変わる
スライド5:倍率が変わると実際の視野の広さは変わるスライド5のように、倍率が高くなると接眼ミクロメーターの1目盛りの長さは小さくなります。
上記のような考えの道筋を理解しておくことで、次回からは知識問題として解けるようになるでしょう。なお、『4分の1になる。』という回答は、不正解です。気になる方は、下の注意点をお読みください。
上述の考え方をすると、「倍率が4倍大きくなったときは、接眼ミクロメーターの1目盛りの長さは4分の1になりそうだから、4分の1に小さくなるではだめなの?」と思う生徒もいるかもしれません。上記の解説だけで考えるとそうなりますが、実際の顕微鏡観察では、倍率が変わるたびに公式を使って接眼ミクロメーター1目盛りの長さを求め直す必要があります。顕微鏡の構造上、このようにするしかないそうです。私は顕微鏡のしくみに全く詳しくないので説明できませんが、もし詳しい方がいましたらコメントでお知らせください。
さりげなく書きましたが、“倍率が変わったときの視野の面積はどう変わるか”または“倍率が変わったときの視野の一辺はどう変わるか”は、定期テストや入試問題でよく見る問題です。重ねて言いますが、考え方を理解しておきましょう。
問4.図を読み取って計算するだけ!
図1の倍率で接眼ミクロメーターを使ってある植物細胞を観察したところ、図2のように見えた。この細胞の長径を求めなさい。割りきれない場合は、小数点第二位を四捨五入しなさい。
この問題は、図の読み取り&計算問題です。図2の植物細胞の目盛り数を読み取って、長さを計算する問題でした。ただし、問2を正しく解けて、接眼ミクロメーター1目盛りの長さがわかっていることが前提となります。
図を正しく読み取ると、植物細胞の長径は細胞壁も含めて接眼ミクロメーターで18目盛りあることがわかります。あとは、この目盛り数に接眼ミクロメーター1目盛りの長さをかけるだけです。なので、計算式は下のようになります。
細胞の長径=(5÷12×10)×18=75μm
計算は以上です。
四捨五入する前の数字を使うことは、他の教科含め生物基礎でも同じです。四捨五入後の数値で計算すると、「4.2×18=75.6μm」となり、正答とはずれてしまいます。
問5.問題文は“原形質流動”の説明!
図2の植物細胞を観察していると、内部で顆粒が動いている様子が見られた。この現象名を答えなさい。
この問題は知識問題です。問題文の解答となる“原形質流動”を答える問題でした。
知識の確認として、引用文を載せておきます。
細胞内部の原形質が流れるように動く現象。エネルギーを消費する運動で、生きた細胞でのみ見られる。オオカナダモの葉の細胞やシャジクモの節間細胞、ムラサキツユクサの雄しべの毛の細胞などがよく観察に用いられる。オオカナダモの細胞では葉緑体の移動として観察できる。細胞内には大きな液胞があるので、葉緑体は細胞膜に沿って移動しているように見えることが多い。…、以下略。
生物用語集<改訂版>、2018年3月16日発行、駿台文庫
問6.速度は「距離÷時間」!
図2の顆粒は、5秒で接眼ミクロメーター6目盛りを動いていた。このときの顆粒の速度は何μm/秒か。割りきれない場合は、小数点第二位を四捨五入しなさい。
この問題は、計算問題です。原形質流動している顆粒の速度を計算して求める問題でした。
まず、速さの求め方に関して確認しましょう。速さは“距離÷時間”で求まりますが、管理人は『おはじき』という算数の言葉で覚えています。その関係は、次のスライド6のようになります。
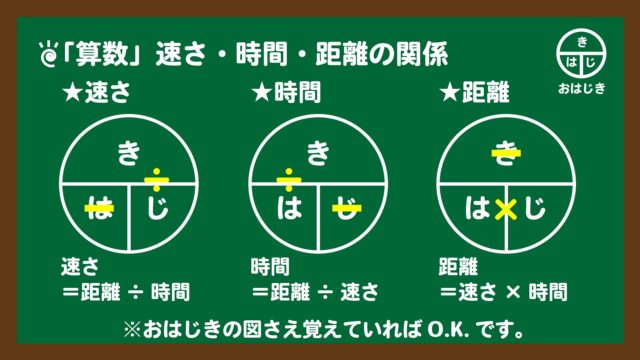 スライド6:速さ・時間・距離の関係(おはじき)
スライド6:速さ・時間・距離の関係(おはじき)スライド6では、横線が“÷”、縦線が“×”を示しています。
では、計算です。
まず、距離を求めましょう。接眼ミクロメーターを6目盛り動いたとあるので、計算式は、
距離={(5÷12)×10}×6
となります。計算式の{}の部分は、接眼ミクロメーター1目盛りであることを、問2で求めました。
そして、時間は5秒だとわかっているので、速さの計算式は、
速さ
=距離÷時間
={(5÷12)×10}×6÷5
=5μm/時間
となります。
算数の『おはじき』の関係を覚えておこう。理系高校生物を履修予定の人は、神経伝導・伝達の典型問題で使うので、必ず覚えておこう。
補足内容
追加問題の紹介
2020年度センター試験でミクロメーターの計算問題がありましたが、この記事で紹介した典型パターンとはやや異なるものでした。詳しくは、下の内部記事にてご覧ください。

対物ミクロメーターの目盛りは、実寸(1目盛り10μm)である。
重要:公式の導き方
スライド1の図1にあるように、接眼ミクロメーターの目盛りと対物ミクロメーターの目盛りが一致する場所は(出題の際は)少なくとも2点あります。これは、それぞれの目盛り数分の長さが一致すると捉えることができます。この考え方を利用すると、
接眼ミクロメーターの1目盛りの長さ × 接眼ミクロメーターの目盛り数
={対物ミクロメーターの1目盛りの長さ(10μm) × 対物ミクロメーターの目盛り数}
という、長さが同じことについての計算式を立てることができます。そして、上記計算式を接眼ミクロメーター1目盛りの長さについて変形すれば、公式の出来上がりです。
2023.05.02、追記。
単位で覚える“速さ・時間・距離”の関係
『おはじき』を使わなくとも、単位で“速さ・時間・距離”の関係を導くことが簡単にできます。それをさらっと紹介しておきます。
- 速さの例:m/h(メートルパー1時間、または1時間分のメートル)
- 時間の例:h(1時間)
- 距離の例:m(メートル)
速さ×時間=(m/h)×h=m(距離)
総括
ミクロメーターのテーマは、光学顕微鏡の計算問題として登場します。ちなみに光学顕微鏡の計算問題としては、倍率を変えたときの視野の広さがどう変わるかというものも登場します。光学顕微鏡の基本的な問題とともにこちらのリンクに問題を用意しておいたので、合わせて勉強するとよいかもしれません。
勉学に励む学生は、すべての公式を覚えておかないといけないと思っていると思います。もちろん公式を素直に覚えることができるのであれば問題がないのでしょうが、あまりの公式の多さに難儀することも多いことでしょう。なので、語呂合わせで覚えたり、公式の導き方の考えを理解するなど、工夫できるところは工夫して問題に取り組めるようになった方が賢いやり方だと思います。丸覚えでなく、理解しながら取り組むようにするとよいでしょう。
おわりに
アンケートにご協力ください!
もっとご協力頂けるなら、アンケートページでお答えください。

お役立ちの“まとめ記事”紹介




ページ下でコメントを受け付けております!
下にスクロールすると、コメント欄があります。この記事の質問や間違いの指摘などで、コメントをしてください。管理人を応援するコメントもお待ちしております。なお、返信には時間がかかる場合があります、ご容赦ください。
以上でこの記事は終わりです。ご視聴ありがとうございました。







3.2×26は73.2ではなく83.2だと思いますが…
ミスのご指摘ありがとうございます。
単純ミスをしていて、申し訳ありません。
2018年8月27日18時に修正させていただきました。
問4はなぜ、掛け算で出す問題なのにも関わらず、割り切れない場合は四捨五入しろと書いてあるのでしょうか?もしくは、何故四捨五入しろと書いてあるのに問2の四捨五入した値をかけて計算してはいけないのでしょうか?
ゆゆ 様
閲覧およびご質問ありがとうございます。
とても良い観点でのご質問で、しばらく考えましたが、下記くらいの考えにしか至りませんでした。
【1つ目のご質問】
・問4では問2の分数(割り算)を用います。
・問4では誤りを誘導するために、四捨五入の文面を入れています。
【2つ目のご質問】
・四捨五入した値を使うことは、不正確な数字を使うことになり、正確さに欠けてよくないです。
ご納得できない場合、他のサービスをご利用ください。
おそらく、数学・物理・化学の先生が頼りになると思います。
管理人シカマルより
追記です。
四捨五入に関する科学のルールは、
・解を四捨五入することはある。
・計算式に四捨五入した値は用いない。
というものではないかと、経験則をもとに考えました。
ただ、改めて思うと、この“ルール”はいつ習得するものなのかはわかりませんでした。
しかし、入試問題では特別の断りがないことが普通のようなので、高校生は習得しているものとされているのかもしれません。
管理人シカマルより