今回は、「高校生物」の第5編の“生物の進化と系統”に登場するハーディー・ワインベルグの法則と遺伝子頻度の計算問題の解き方を紹介します。定番問題のポイントをわかりやすく解説しているので、是非活用してください。
※問題の編集を行いました。スライド１からは、プレテスト改題は削除して代わりに追加問題を加えています。（2019年6月中旬）
今後、遺伝の法則の用語「優性・劣性」は「顕性・潜性」と言い換えられる予定になっているそうです。入試問題でも言い換えられる可能性が高いので、「顕性・潜性」の表現にも慣れておくとよいでしょう。
演習問題
まずは演習問題として、下のスライド１を解いてみましょう。目標解答時間は、基本問題で5分、応用問題で10分です。時間が経っても解けない場合は、すぐに解答・解説を見ましょう。
スライド１：ハーディー・ワインベルグの法則と遺伝子頻度の計算問題解き具合はどうでしたか。管理人の主観としては、
- 基本問題は、難なく解けてほしい。
- 応用問題は、見たことがないのであれば解けなくともよい。
というような思いがあります。以下の解答解説を読んで、応用問題もできるようになりましょう。
解答
問１．p：0.6、q：0.4
問２．120人
問３．p：0.71、q：0.29
問４．122人
問５．A島：２％、B島：１％
問６．A型遺伝子の頻度…1／2、B型遺伝子の頻度…1／5、O型遺伝子の頻度…3／10
解説
問１．遺伝子頻度を求める基本的な問題！
ある生物の対立遺伝子には、優性遺伝子Aと劣性遺伝子aが存在する。この生物の集団αでは、100個体中16個体が劣性形質を持っていた。優性遺伝子Aの遺伝子頻度をp、劣性遺伝子aの遺伝子頻度をqとしたとき、pとqの数値を答えなさい。
この問題は計算問題です。遺伝子頻度pとqを求めるというこのテーマの最も基本的な問題でした。
まずは、遺伝子頻度pとqがどのように個体数と関わっているかを理解するところから始めましょう。下のスライド２を見てください。
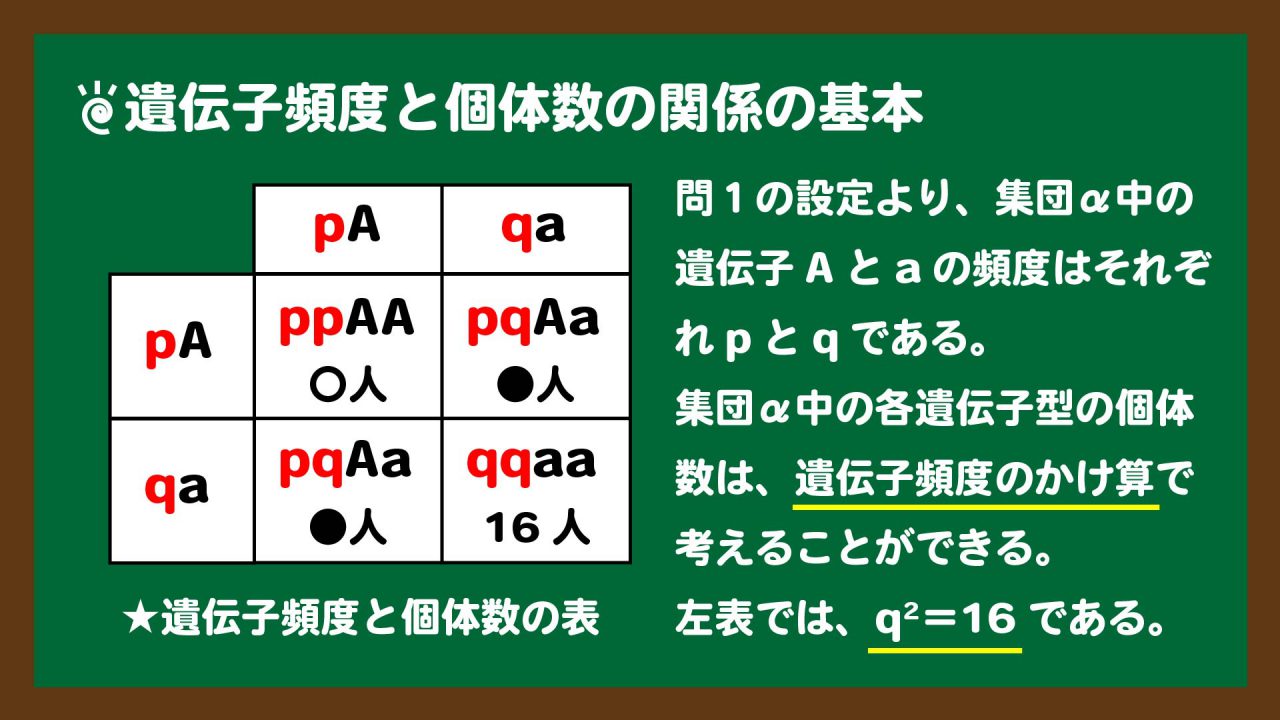
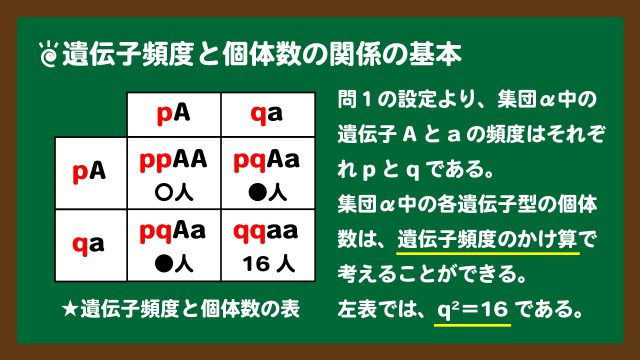スライド２：集団中の個体数は遺伝子頻度のかけ算で考えるまず設問の補足をしておきます。今回は優性遺伝子Aの遺伝子頻度はp、劣性遺伝子の遺伝子頻度はqとなっています。設問の設定では出ませんでしたが、p＋q＝1です。1つの対立遺伝子の遺伝子頻度の総値は、必ず1になります。つまり、pやqは小数点の値になるとも言うことができます。
遺伝子頻度の個体数を求めるときは、スライド２の左表のようなものをつくる必要があります。このとき、集団中の各遺伝子型は遺伝子頻度のかけ算で考えることができます。なので例を挙げると、
- 遺伝子型AAの人数＝pp×全個体数
- 遺伝子型Aaの人数＝2pq×全個体数
- 遺伝子型aaの人数＝qq×全個体数…(b)
という考え方になります。
さて、スライド２の文末に書きましたが、qqaa＝16となっています。これを上の箇条書きの(b)に代入してみましょう。このとき、全個体数100も代入してください。すると、
- 16＝qq×100 → qq＝16／100
となります。あとは、計算をするとq＝0.4と求まります。また、p＋q＝1だったので、p＝0.6も求まり、問１は解くことができました。
遺伝子頻度を求める計算は基本なので解けるようになろう。意識するとよいのは、p2あるいはq2が二乗の数値になっているか見極めることです。
問２．次世代の特定の遺伝子型の個体数を答える基本問題！
問１の集団αの次世代集団であるβは、250個体の集団である。このとき、遺伝子型がAaである個体の数を答えなさい。ただし、ハーディー・ワインベルグの法則が成り立っているとする。
この問題は計算問題です。問１の遺伝子頻度（p＝0.6、q＝0.4）を使うので、問１の続問と言うことができるでしょう。
問２の設問のように、次世代（集団β）の個体のうち特定の遺伝子型をもつ個体数を求めるためには、ある条件が成り立ってさえいれば前世代（集団α）の遺伝子頻度を使うことができます。その条件が、ハーディー・ワインベルグの法則です。この問２ではハーディー・ワインベルグの法則が成り立つと書いてあるので、全世代である集団αの遺伝子頻度p＝0.6とq＝0.4を次世代の集団βでも使うことができます。
問１の解説でも書きましたが、集団βでも特定の遺伝子型の個体数は次の式で求めることができます。
- 遺伝子型AAの人数＝pp×全個体数
- 遺伝子型Aaの人数＝2pq×全個体数…(c)
- 遺伝子型aaの人数＝qq×全個体数
式cに数値を代入してみましょう。すると、下のスライド３のようになります。
スライド３：問２の計算式このようになり、答えを求めることができました。
ちなみに2pqであることを不思議に思う人もいるかもしれません。なぜ2がついているのかと理解できていない人もいるでしょう。理由は簡単です。メンデル遺伝で交配を行う際に、pqの枠が2つあるからです。図で見たい方のために、スライド２を少し加工したものを下にスライド４として載せておきます。
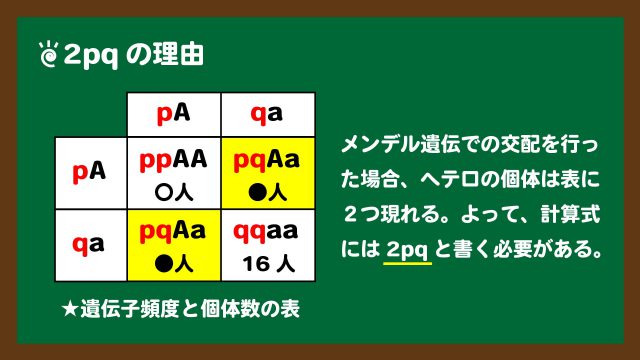スライド４：2pqの理由やはり交配の表をつくることが大事だということですね。
次世代の個体数を求めるとために前世代の遺伝子頻度が使えるのは、ハーディー・ワインベルグの法則が成り立っているときだけである。
問３．絶滅による遺伝子頻度の変化を答える応用問題！
仮に、環境の大きな変動によって、問１の集団αの劣性ホモ個体がすべて絶滅したとする。この集団の次世代γ（ガンマと読む）の遺伝子頻度はどのように変化するか。集団γの優性遺伝子Aと劣性遺伝子aの遺伝子頻度を答えなさい。ただし、数値小数点第三位を四捨五入して答えなさい。
この問題は計算問題です。遺伝子頻度を求める問題ですが、問１の集団αの劣性ホモ個体が絶滅したという設定が付け加えられています。このような問題は、このテーマで割とよく見かける問題パターンです。
まず、問３を解く順番から確認しましょう。以下の２つの手順が必要になります。なお、劣性ホモ個体が絶滅した集団を“集団α’”と扱うことにします。
- 劣性ホモ個体が絶滅した集団α’の遺伝子Aとaの数を数える。
- 集団α’の遺伝子Aとaの遺伝子頻度を求め、集団γの遺伝子頻度として答える。
では、まず手順①から理解していきましょう。集団α’の遺伝子を数えるためには、下のスライド５のようなことを行います。
スライド５：遺伝子の数え方このように集団α’の遺伝子を数えることができます。遺伝子Aは120個、遺伝子aは48個だとわかりました。
次に手順②です。遺伝子数から遺伝子頻度を算出することができます。そのステップは、下のスライド６のようになります。
スライド６：変化した遺伝子頻度を求めるこの変化した遺伝子頻度が、そのまま集団γの遺伝子頻度として扱うことができます。なお、“集団α’から次世代の集団γが生じるときにハーディー・ワインベルグの法則が成り立っている”という記載はありませんが、問題はありません。設問の意図を組むと、「集団αから次世代集団γが生じるときは、（ハーディー・ワインベルグの法則が成り立っていないので）そのまま集団αの遺伝子頻度を使うことはできないよ。」というような感じになります。
集団に絶滅などの変化があった場合、その集団の遺伝子頻度は変わる！
問４．変化した遺伝子頻度で次世代の個体数を答える応用！
問３の集団γが300個体の集団だったとする。このとき、遺伝子型がAaである個体の数を答えなさい。また、個体数は四捨五入をして整数で答えなさい。
この問題は計算問題です。計算方法は問２と同じですが、やはり問３で求めた遺伝子頻度が必要となるので、問３の続問と言うことができるでしょう。
再び登場しましたが、集団の個体数は下の箇条書きのようになります。
- 遺伝子型AAの人数＝pp×全個体数
- 遺伝子型Aaの人数＝2pq×全個体数…(e)
- 遺伝子型aaの人数＝qq×全個体数
この(e)を使って計算してみましょう。すると、下のスライド７のようになります。なお、pとqの遺伝子頻度は、四捨五入する前のものを利用した方がより正確です。
スライド７：問４は変化した遺伝子頻度で個体数を求めるこのようにして、答えを求めることができました。
変化した遺伝子頻度で集団の特定の遺伝子型の個体数を求める！
問３で答えた『p≒0.71』と『q≒0.29』を使って計算すると解答の値は『123.54』となりますが、この計算は正確ではありません。『≒』という記号を使っているように、pとqの値が正確な数値ではないからです。pとqの数値はスライド６で紹介した分数として用い、計算して下さい。
なお、問題文中に『ただし、値は問３で答えた近似値を用いること』とあれば、近似値で計算してもよいです。
問５．保因者の割合を計算する応用計算問題！
あるヒトの病気は常染色体劣性の遺伝様式を示す。この遺伝子に対して遺伝子平衡が成立するA島では１万人に１人の割合でこの病気の人が出現し、B島では４万人に１人の割合でこの病気の人が出現した。A島とB島における保因者の割合（％）を求めなさい。
A島
1/10000＝1/100×1/100より、
優性遺伝子の遺伝子頻度p＝0.99、劣性遺伝子の遺伝子頻度q＝0.01
保因者＝10000×2pq＝198人
パーセンテージ＝198÷10000×100≒2(%)（または＝1.98（％））
※有効桁数にご注意ください。
B島
1/40000＝1/200×1/200より、
優性遺伝子の遺伝子頻度p＝0.995、劣性遺伝子の遺伝子頻度q＝0.005
保因者＝40000×2pq＝398人
パーセンテージ＝398÷40000×100≒1(%)（または ＝0.995（％））
※有効桁数にご注意ください。
※1：より詳しい解説は準備中です。
※2：アノマロカリス様、間違いのご指摘ありがとうございます。
※3：閲覧している皆様におかれましては、保因者の意味を辞書でお調べください。
保因者：（準備中）
問６．血液型のテーマも入った応用計算問題！
あるヒトの集団においてABO式血液型を調べたところ、A型が55％、B型が16％、O型が9％、AB型が20％であった。このヒト集団ではハーディー・ワインベルグの法則が成り立つものとして、このヒト集団におけるA型遺伝子、B型遺伝子、O型遺伝子の頻度を求め、それぞれ最も簡単な分数で求めよ。
【簡単な解説】
A型遺伝子の遺伝子頻度をx、B型遺伝子の遺伝子頻度をy、O型遺伝子の遺伝子頻度をzと文字で仮定する。
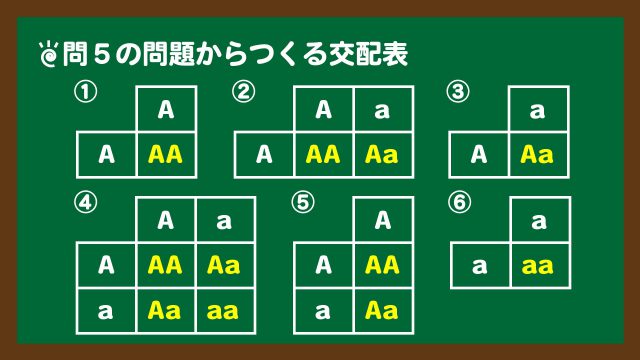
集団の交配表をつくると、以下のようになる。
| xA | yB | zO | |
| xA | x2AA | xyAB | xzAO |
| yB | xyAB | y2BB | yzBO |
| zO | xzAO | yzBO | z2OO |
よって、集団の血液型の頻度は、
- A型：x2＋2xz＝0.55 …(1)
- B型：y2＋2yz＝0.16 …(2)
- AB型：2xy＝0.20 …(3)
- O型：z2＝0.09 …(4)
となる。
ここで、式(4)を平方根の計算をしてみると、
- z＝0.3（3／10）
となる。これを式(2)に代入して計算するとyの値が求まり、最後にyの値を(3)に代入するとxの値が求まる。
※より詳しい解説は準備中です。
遺伝の問題のまとめ記事
遺伝の問題について、管理人がつくった問題解説をまとめました。是非ご活用ください。
総括
ハーディー・ワインベルグの法則と遺伝子頻度の問題は頻出テーマです。なぜ頻出なのかというと、高校生物第５編の計算問題が、今回の問題と“分子進化”くらいしかないからです。なので、是非とも解けるように慣れてほしいと思います。
分子進化の記事も、合わせて読んでみるとよいでしょう。下の記事は、管理人がつくったものです。ぜひ、参考にしてください。
https://biology-manabiya.net/ch-29/
なお、ハーディー・ワインベルグの法則と遺伝子頻度の計算問題は、プレテストにも登場しています。その内容としては、超難問でした。おそらく解答解説を読んでも理解することに骨が折れると思います。大学入学共通テストの対策として、思考力を磨く努力をすることがよいと思われます。
プレテストの内容は、下のリンクから見ることができます。独立行政法人大学入試センターのページになります。
おわりに
アンケートにご協力ください！
もっとご協力頂けるなら、アンケートページでお答えください。
お役立ちの“まとめ記事”紹介
ページ下でコメントを受け付けております！
下にスクロールすると、コメント欄があります。この記事の質問や間違いの指摘などで、コメントをしてください。管理人を応援するコメントもお待ちしております。なお、返信には時間がかかる場合があります、ご容赦ください。
以上でこの記事は終わりです。ご視聴ありがとうございました。
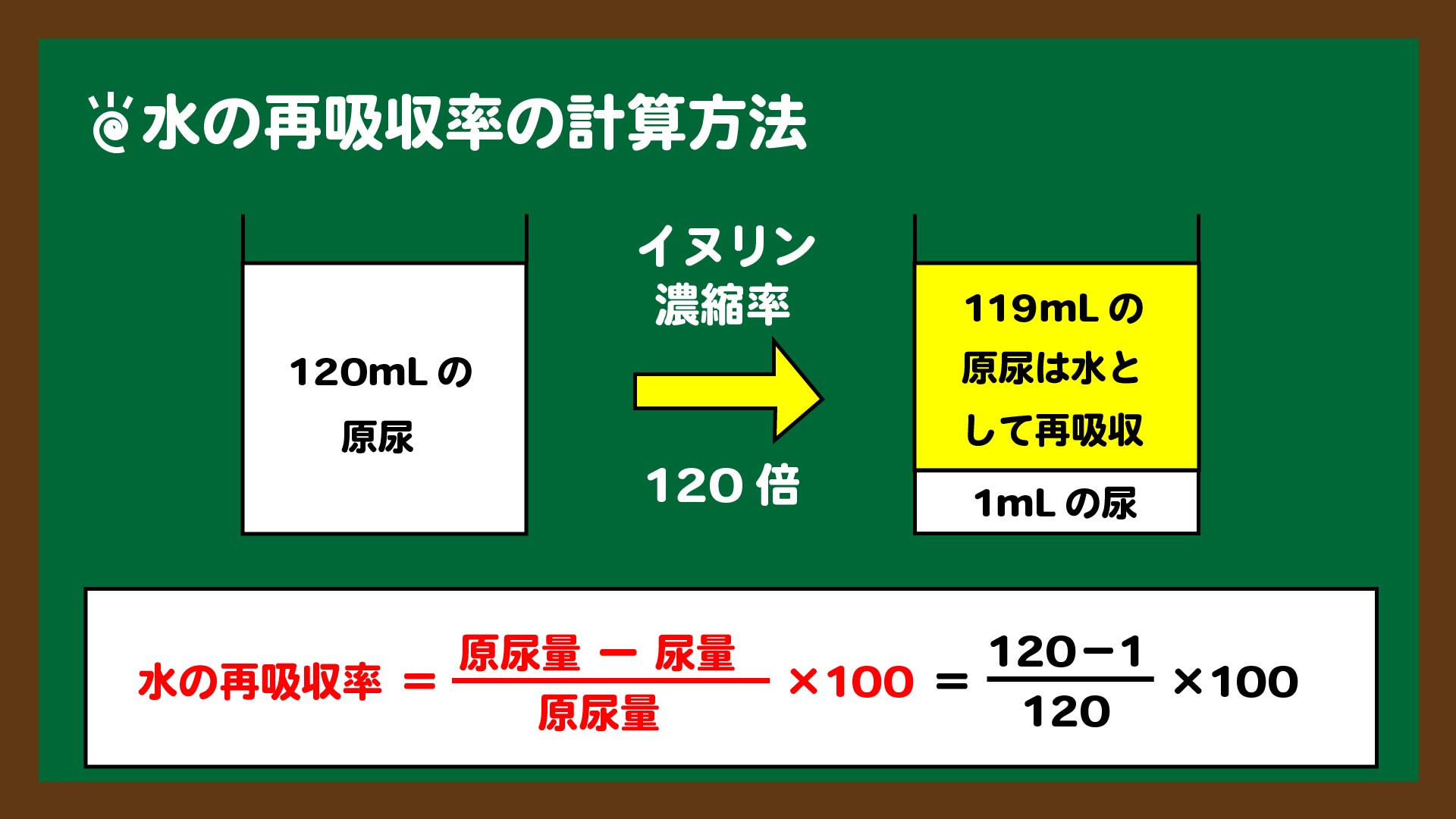
問四の計算が123.54という数値になるんですけど、自分のミスですかね、、、
すみません、
CD 様
コメントありがとうございます。
問３で答えた遺伝子頻度（p≒0.71、q≒0.29）を用いて計算すると、問４の計算結果は『123.54』になると思います。
しかしながら、この２つの値は『≒』なので、問４の計算でのpとqの数値はスライド６にある分数を使う方が正確です。
そうすると、計算結果は『122.44…』というようになります。
管理人シカマルより
なるほど。分かりました。ありがとうございます！
なぜ保因者の中に劣性ホモが含まれるのですか？
クックソニア 様
コメントありがとうござます。
ご質問の内容を問５のことと推察してお答えします。
問題文中に『病気が常染色体劣性の遺伝様式を示す』とあります。
このとき、遺伝子をてきとうに優性遺伝子Aと劣性遺伝子aと置いてみます。
この場合の遺伝子型を考えると、優性形質AAとAa、劣性形質aaとなります。
その際、保因者とは、『劣性遺伝子』を持つ人のこととなり、Aaとaaの遺伝子型の人を指します。
よって、保因者は“遺伝子をヘテロで持つ人”と“劣性ホモで持つ人”が該当します。
管理人シカマルより
回答ありがとうございます！
理解できました(✿^‿^)
常染色体上の遺伝子ということを読み落としていました。
伴性遺伝の場合、女性の中での保因者を考えるときはヘテロのみが保因者として数えられていて、それと同じように考えてしまい間違ってしまいました。
問４のAaの個体数を求める際に２pqで考えるのはなぜですか？
集団αの劣勢ホモ個体が絶滅したとき次世代である集団γをメンデルの法則で考えたとき２pqとなる理由がわからないです。
初歩的なことかもしれないですが、お願いします。
まりも 様
閲覧およびコメントありがとうございます。
集団において遺伝子頻度がわかっているとき、個体数（の期待値）は、個体数と遺伝子頻度から導くことができます。
優性遺伝子(A)の遺伝子頻度がp、劣性遺伝子(a)の遺伝子頻度がqのとき、個体数の計算方法は、
・優性ホモ(AA)：集団の全個体数×pp
・ヘテロ(Aa)：集団の全個体数×2pq
・劣性ホモ(aa)：集団の全個体数×qq
となります。
上記の箇条書きにあるpp、2pq、qqは、記事中のスライド２とスライド４にあるようなメンデル遺伝の交配を元に導くことができます。
ヘテロの個体数を計算する際にpqではなく2pqを用いることについては、スライド４付近で説明している通りで、
パネットの方形を作った際にpqが２つあることが理由になります。
まりも様が躓いているポイントをうまく予想できなかったので、記事中の説明を繰り返す形になってしまい、申し訳ありません。
ご不明な際は、再度のコメントをお願い致します。
管理人シカマルより
問四ではaaが絶滅しているので無視できるのですが、AA×Aaの場合を考えずにAa×Aaだけを考えるということですか？
まりも 様
再度のご質問、ありがとうございます。
交配に関して不明な点があると察してお答えします。
集団αは劣性ホモが絶滅しているため、αにはAAとAaの個体が存在することになります。
なので、集団αが次世代の集団γを生み出すために交配する場合は、
・AA×AA
・AA×Aa
・Aa×Aa
の３つ交配のパターンが存在することになります。
aa×aaの交配がないため、集団γの遺伝子頻度は集団αから変わってしまいます。
ちなみに、上記のような交配のパターンがあることと、集団内の遺伝子型の個体数の期待値を求めることは、別問題です。
先のコメントで述べた通り、集団内の遺伝子型は、集団の個体数と遺伝子頻度から導くことができます。
スライド中のpAとqaという表現は、Aa×Aaの交配のことではありません。
集団に遺伝子Aがpという頻度で存在、遺伝子aがqという頻度で存在し、その組み合わせを考えている形になっています。
強いて言うのであれば、pAとqaの組み合わせは、上記の交配パターン全てを網羅していることになります。
以上のことから改めてご質問に答えますと、Aa×Aaだけ考慮しているわけではありません。
pAとqaの組み合わせは、Aa×Aaの交配のことではありません。
pAとqaの組み合わせは、集団内の遺伝子型の個体数を計算する方法になります。
長文になり、失礼しました。
今回は、まりも様が躓いている点が少し見えたので、文章が長めになってしまいました。
ご不明な場合は、再度コメントにてご質問ください。
管理人シカマルより
自分がわかっていなかったことがわかりました！
ありがとうございます！
問5の問題ですが、劣性ホモは保因者ではなく発症者になるので計算に含めないのではないですか？
アノマロカリス 様
閲覧およびコメントありがとうございます。
おっしゃる通りで、私が保因者と発症者を誤解していました。
情けない限りで、申し訳ありません。
ご指摘いただいて、本当にありがとうございます。
急ぎ記事を最低限修正しましたので、ご確認いただければと思います。
今後とも高校生物の学び舎をよろしくお願い致します。
管理人シカマルより
突然すみません。質問がありコメントさせて頂きます。
問3のスライド5で，「AAの人はA遺伝子を2つ，Aaの人はA遺伝子を1つもつ」という部分が分かりません。
なぜA遺伝子を2つもつと2をかけなければいけないのでしょうか。
36×2＋48×1＝120という計算式になる意味がどうしても分かりません。
出来ましたら具体的に詳しく教えて頂けますと幸いです。
何卒よろしくお願い申し上げます。
あかり 様
閲覧およびコメントありがとうございます。
参考資料を作りましたので、ご確認ください。
（見当違いな解説だったら申し訳ありません…。）
今後とも高校生物の学び舎をよろしくお願い致します
管理人シカマルより
問３のｑの遺伝子頻度の48/128の計算結果が、37.5になるんですけどあってますか？
まちがえてました 48/168でした！ごめんなさい！