「高校生物」盲斑の測定実験の計算問題の解き方を解説
この記事では、高校生物の第6章「動物の反応と行動」に登場するヒトの眼の“盲斑の測定実験の計算問題”の解き方について解説を行っています。日常学習のお役に立てたら幸いです。
なお、この問題を解く前提として“眼の構造”を習得している必要があります。眼の構造について自信がない方は、下の内部リンクで学習してみてください。画像のPDFをダウンロードすることができます。
https://biology-manabiya.net/hs-biology-k/
問題
では、まず問題を解いてみましょう。下のスライド1が問題用紙になります。標準解答時間は10分です。10分経っても解けなかった場合は、解答と解説を見ましょう。
解き具合はどうだったでしょうか。問1から問3まで、いずれも計算問題です。ただ、数学の“図形の相似”を使う必要があり、高校生物と数学の分野横断的な問題でした。解き方は単純な方なので、解けなかった方は以下の解答・解説を見て復習しましょう。典型問題なので、必ず解けるようになりましょう。
解答
問1.4.5mm
問2.0.12cm
問3.0.58cm
解説
必要な知識・経験(①・②)
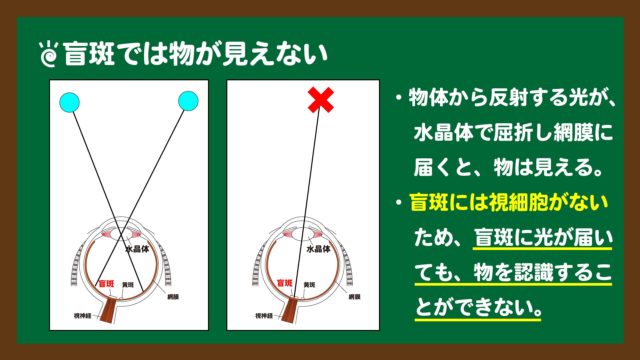
①盲斑では物が見えない
物が見えるということを改めて解説すると、次のようになります。
物体から反射してきた光が、角膜と水晶体を屈折して網膜に届くと、視細胞が光を感知し、神経を通って脳の視覚野で情報が処理されて、物が見える。
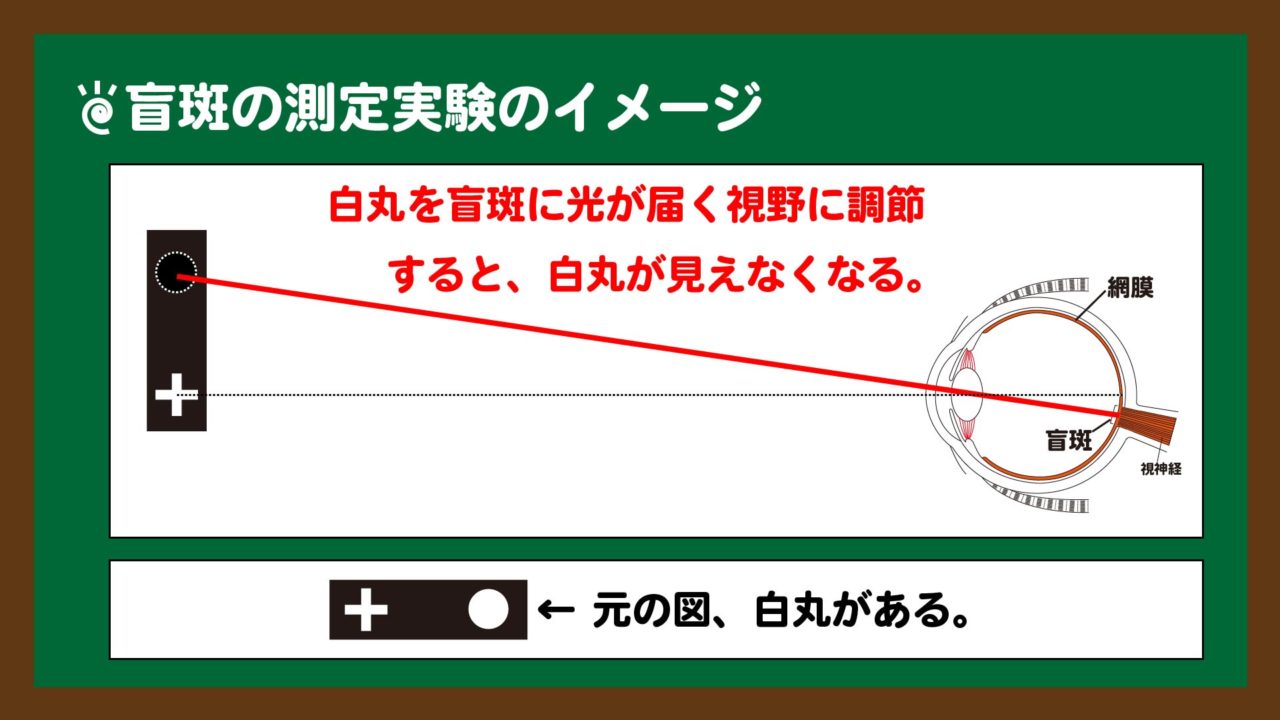
この問題を解く上で必要な知識は、上の解説に加えて、「盲斑には視細胞がないため、盲斑では“物を見る”ことはできない。」ということです。下のスライド2が、そのイメージ図になります。
この知識を活かして、実際に盲斑の測定実験を行うと、次のスライド3のようなイメージになります。
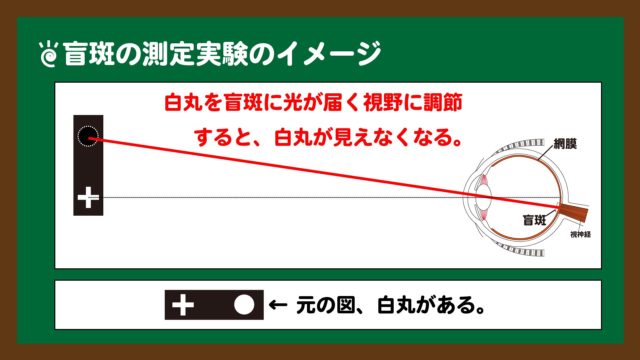 スライド3:盲斑の測定実験のイメージ
スライド3:盲斑の測定実験のイメージ今回の問題においては、スライド3の図を考慮することができることが、1つのポイントとなります。
スライド3のイメージ図で理解できるかもしれませんが、片目で物が見えない範囲があることは実際に経験してみた方がよくわかると思います。教科書や資料集の図を使って、是非とも経験してみてください。
②相似図形における比(数学要素)
今回の問題を解くためにもう1つ大事なポイントは、次の数学的な知識になります。
相似条件にある2つの図形においては、辺の比を立てることができる。
問題で使う数式のイメージ図としては、下のスライド4のようなものになります。
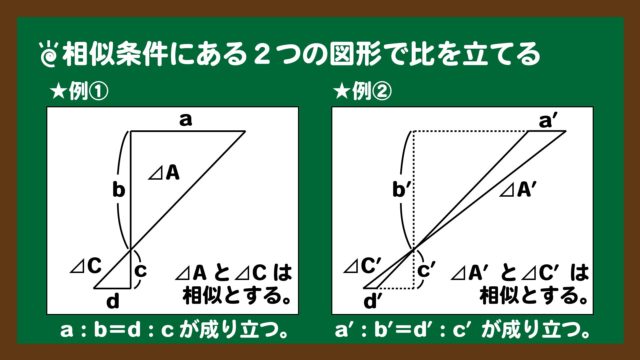 スライド4:相似条件にある2つの図形で比を立てる(例)
スライド4:相似条件にある2つの図形で比を立てる(例)必要な数学の知識はこの程度です。では、解説に入りましょう。
スライド4がいまいちわからない方は、学校や塾の数学の先生に質問してみるとよいでしょう。ちなみに、図形の相似の単元は、中学校の内容だったかもしれません。
問1.黄斑と盲斑の間の距離を求める典型計算問題!
この問題は計算問題です。問題文にあるように、黄斑と盲斑の間の距離を求める計算問題でした。
上述の必要な知識・経験を理解した上で話を進めます。実験1の内容をイメージにしたものが、下のスライド5になります。
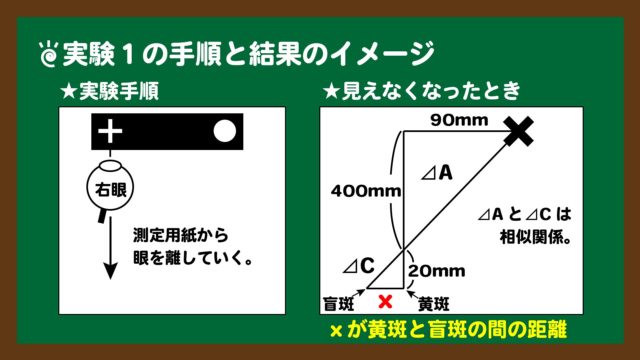 スライド5:実験1の手順と結果のイメージ
スライド5:実験1の手順と結果のイメージ★実験1の結果において、
- 測定用紙と右眼の距離:400mm
- 水晶体と黄斑の距離:20mm
- 測定用紙上の+印と〇印の距離:90mm
実験内容は、スライド5の左の図にあるように、+印の真正面に右眼を合わせ、左眼を閉じた状態で測定用紙から右眼を離すようなものでした。結果、〇印が見えなくなったときには、スライド5の右図のような図形を組み立てることができます。図中の辺xが盲斑と黄斑の間の距離に相当します。
では、xを求める計算式を立てましょう。スライド5の右図において、△Aと△Cは相似関係にあるので、計算式および計算結果は次のようになります。
【計算式】
90:400=x:20
x=90×20÷400
x=4.5(mm)
以上のような形で簡単に計算することができます。リード文の最初に「計算結果は有効数字二桁で答えなさい。」とあるのをお忘れなく。
スライド5の右図では、黄斑と盲斑の間の辺を直線にしていますが、実際の眼の構造では曲線になります。理由は単純で、眼の構造が球状であるためです。しかしながら、高校生物の問題では基本的には直線として扱い、2つの三角形の相似条件から黄斑と盲斑の間の距離を求めることになります。この値は、“近似値”として扱うのかもしれませんね。
実験結果を相似関係の2つの三角形として捉え、計算する。
問2.盲斑を円として捉える計算問題!
この問題は計算問題です。盲斑を点ではなく円として捉え、その直径を求める計算問題でした。
実際の眼の構造でも、盲斑はほぼ円状です。問1で点として扱ったのはあくまで“〇印が見えなくなったとき”を点としただけであり、〇印が見えなくなる高さにはゆとり(幅とも表現?)があります。よって、この問2のように、盲斑の直径を求める問題も定期テストや入試では出題されます。
では、実験2を解釈して、計算するうえで必要な図形を考えましょう。実験2の内容をイメージにしたものが、下のスライド6になります。
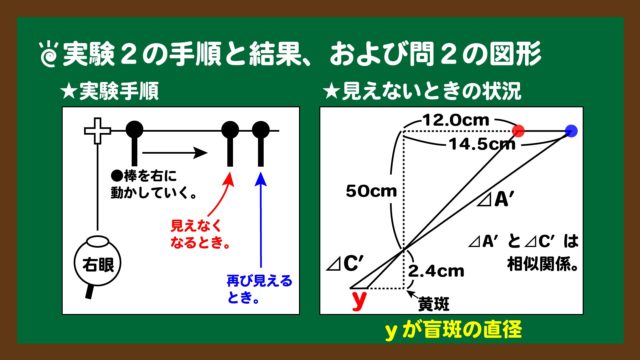 スライド6:実験2の手順と結果、および図形
スライド6:実験2の手順と結果、および図形★実験2の結果において、
- +印から右眼までの距離:50cm
- 黒点が見えなくなったときの位置は、+のマークから12.0cm。
- 再び黒点が見えるようになった位置は、+のマークから14.5cm。
- ヒトの眼球の直径:2.4cm
実験内容は、スライド6の左の図にあるように、生徒Aが+印の真正面に右眼を合わせ、かつ左眼を閉じた状態にし、生徒Bが黒丸が付いた棒を+印から水平に右に動かすようなものでした。結果、〇印が見えなくなったときと再び見えるようになったときがあり、これらはスライド6の右図のような図形を組み立てることができます。図中の辺yが盲斑の直径に相当します。
では、yを求める計算式を立てましょう。スライド6の右図において、△A’と△C’は相似関係にあるので、計算式および計算結果は次のようになります。
【計算式】
(14.5-12.0):50=y:2.4
2.5:50=y:2.4
y=0.12(mm)
以上のような形で簡単に計算することができます。リード文の最初に「計算結果は有効数字二桁で答えなさい。」とあるのをお忘れなく。
実験結果を相似関係の2つの三角形として捉え、計算する。
問3.問1の復習(黄斑と盲斑の間の距離の計算問題)!
この問題は計算問題です。内容としては問1と同じで、復習要素として再度問題にしました。
解き方は問1と同じですので、解説は省略して計算式のみ掲載しておきます。なお、計算結果は、設問にある通り有効数字二桁にします。
【計算式】
問3の“黄斑の中心から盲斑に達するまでの距離”をzとおくと、
12.0:50=z:2.4
z=0.576
z≒0.58(mm)
以上です。
総括
盲斑の測定実験の計算は、結果の計算式だけを見ると非常に簡単なものです。しかし、解くに当たっては図形を描き、かつ相似として捉えて比を使う必要があるので、高校生物というよりは数学的な内容になります。このように教科をまたぐ分野横断的なテーマなので、初見の人にとってはそこそこ難しかったかもしれません。わからなかった方は、今回を機に理解に努めましょう。なお、計算式を導くときは、暗記ではなく理解で解けるようになることが望ましいです。
教科をまたぐ問題は、他にもあります。代謝の単元では、反応式の計算に物質量(mol)を使うことは、既に経験しているでしょう。高校生物の範囲以外の知識を使うときは、これも丸暗記ではなく、理解で導けるように努めましょう。
おわりに
アンケートにご協力ください!
もっとご協力頂けるなら、アンケートページでお答えください。

お役立ちの“まとめ記事”紹介




ページ下でコメントを受け付けております!
下にスクロールすると、コメント欄があります。この記事の質問や間違いの指摘などで、コメントをしてください。管理人を応援するコメントもお待ちしております。なお、返信には時間がかかる場合があります、ご容赦ください。
以上でこの記事は終わりです。ご視聴ありがとうございました。