「高校生物」筋肉の張力のグラフと計算の問題の解き方を解説

この記事では、高校生物の第６章「動物の反応と行動」に登場する“筋肉の張力のグラフと計算の問題”の解き方について解説を行っています。日常学習のお役に立てたら幸いです。

問題

では、まず問題を解いてみましょう。下のスライド１が問題用紙になります。標準解答時間は15分です。15分経っても解けなかった場合は、解答と解説を見ましょう。

※本題は問４です。基本ができている方は、問１～問３を無視しても問題ありません。

スライド１：筋肉の張力のグラフと計算の問題

解き具合はいかがだったでしょうか。今回の問題の本題は問４であり、問１と問３は解く上での前提知識の確認となっています。以下の解答と解説を見て、確認をしましょう。

解答

解答は、下のスライド２のようになります。

スライド２：筋肉の張力のグラフと計算の問題の解答

解説

問１．筋肉の構造と収縮に関する基本的な語句埋め問題！

★問１の問題文

筋肉を構成する細胞は( 1 )と呼ばれ、骨格筋は核についてある特徴を持つ。ま
た、細胞内には( 2 )という特有の構造が束になって多数存在する。( 2 )の単位
当たりの構造は、下の図１のようになっている。横紋筋の収縮は( 3 )の間に( 4 )
が滑り込むことによって起こり、この考えは( 5 )と呼ばれる。

この問題は語句埋め問題です。筋肉の構造と収縮を簡単に説明しているリード文の空白を、適切な語句で答える問題でした。

筋肉の基本的な構造に関しては、生物基礎の発展内容（第１章『生物の特徴』）として、次のスライド３のような内容を習得していることが前提となります。

スライド３：生物基礎発展で習得済みの筋肉の内容

これに加えて、高校生物では第６章『動物の反応と行動』で横紋筋の構造を学ぶことになります。学ぶ内容は、次の通りです。

筋肉を構成する細胞は筋繊維（筋細胞）と呼ばれ、多くの筋原繊維を含む。筋原線維は、太いミオシンフィラメントと細いアクチンフィラメントが規則正しく配列し、格子状の構造をつくっている。

これらの内容から、(1)が筋繊維、(2)が筋原線維であると判断することができます。

次に、筋肉の収縮についてです。

筋肉の収縮の定説である滑り説では、筋肉の収縮を次のように説明しています。

横紋筋の収縮は、筋原線維のミオシンフィラメント間にアクチンフィラメントが滑り込むことによって起こる。

図解すると、次のスライド４のようになります。

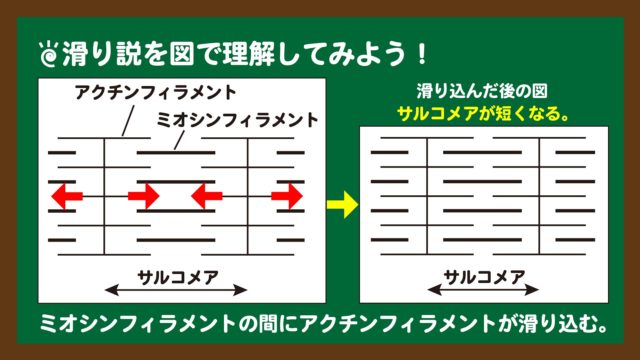スライド４：滑り説を図で理解する

筋原線維の構造については問２の範囲ですが、理解しやすくするためにここでも扱いました。収縮の際は、スライド４の左図にある赤矢印の方向にアクチンフィラメントがミオシンフィラメント間に滑り込みます。

以上の滑り説の内容から、(3)はミオシンフィラメント、(4)はアクチンフィラメント、(5)は滑り説と判断することになります。

滑り説において、滑る主体がミオシンフィラメントとアクチンフィラメントのどちらなのか混乱している方がいるようです。“ミオシンフィラメント間にアクチンフィラメントが滑り込む”、つまり滑る主体はアクチンフィラメントだと、改めて理解しておきましょう。

問２．骨格筋の筋繊維は多核である！

★問２の問題文

下線部（骨格筋は核についてある特徴）について、特徴を簡潔に説明しなさい。

この問題は論述問題です。骨格筋の筋繊維における核の特徴を簡潔に答える問題でした。

問１のスライド３②で紹介したように、“骨格筋の筋繊維は多核である”という特徴があります。それを答えればよいだけの問題でした。

問３．筋原線維の模式図の語句埋め問題！

この問題は語句埋め問題です。筋原繊維の単位構造である図１の(a)～(f)の構造を答える基本的な問題でした。

図１の用語を穴埋めすると、下のスライド５のようになります。

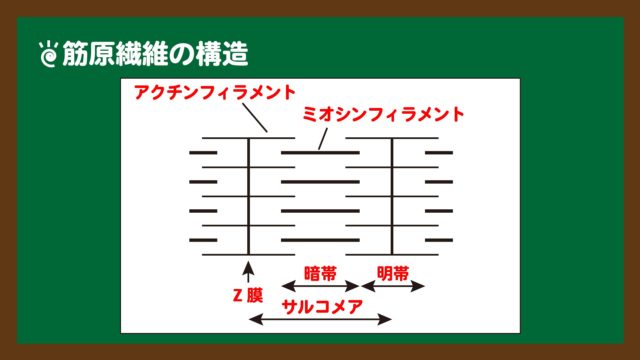スライド５：筋原線維の単位構造

スライド５の用語に関しては暗記するしかないので、この場で改めて覚えましょう。

問４．筋肉の張力のグラフと計算の問題（今回の本題）

この問題は、文章読み取り・グラフの読み取り・計算の総合問題です。リード文中の設定やグラフを読み取って計算するというような、かなり難易度の高い問題でした。

いろいろと説明することはありますが、まずは下のスライド６とスライド７を見てほしいと思います。

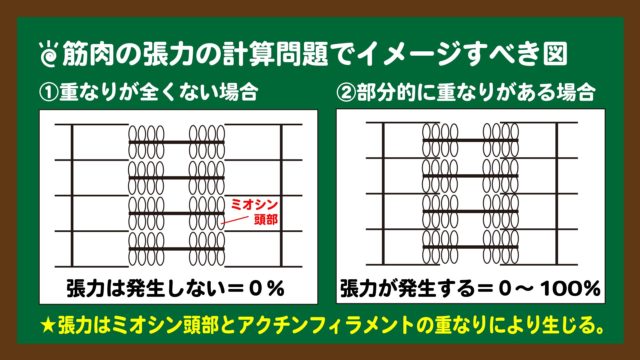スライド６：張力発生時の筋原線維のようす①と②

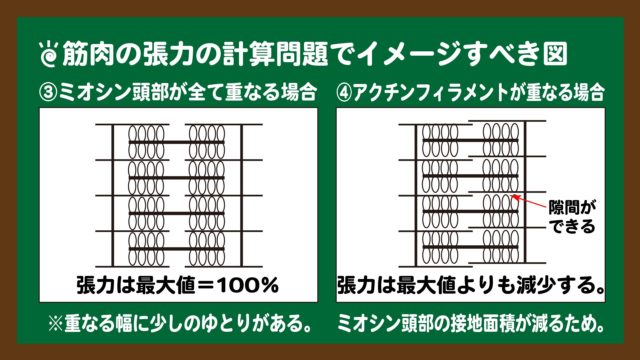スライド７：張力発生時の筋原線維のようす③と④

※スライド６・７を見て勘付いた方は、もう一度問題を見てチャレンジしてみましょう。解説を読むよりもヒントを元に自力で考えることが、自身の実力に結びつきます。

では、スライド６・７の①～④の図を元に、解説をしていきます。

まず、問４のリード文には、次のようなヒントがありました。

【問４リード文中の設定文】

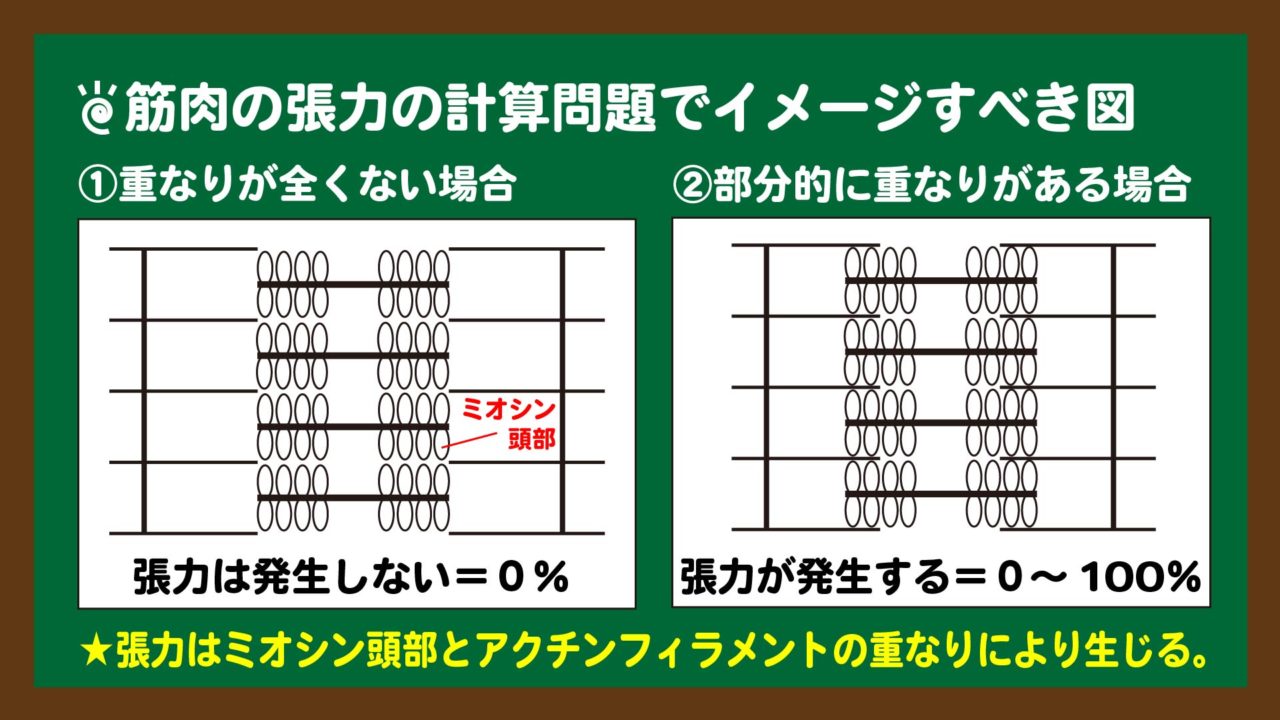
アクチンフィラメントとミオシンフィラメント（の頭部）の重なりが多いほど張力は大きくなる。
相対張力が100%となるサルコメアの長さには、少しの幅（ゆとり）がある。
アクチンフィラメントどうしが重なる場合は、抵抗が増して張力は減少する。

それぞれの意味を読み解いてみましょう。

設定文①は、スライド６中の①と②の場合に相当します。張力はミオシン頭部とアクチンフィラメントの重なりによって生じるので、設定文①はそのことを少し噛み砕いて説明していることがわかります。これを元にサルコメアの長さを図２から読み取ると、2.2から3.6μmの間を指すことになります。

次に設定文②は、スライド７中の③の場合に相当します。問題文中の“幅がある”という表現の解釈が難しいところですが、図解すると下のスライド８のようになります。

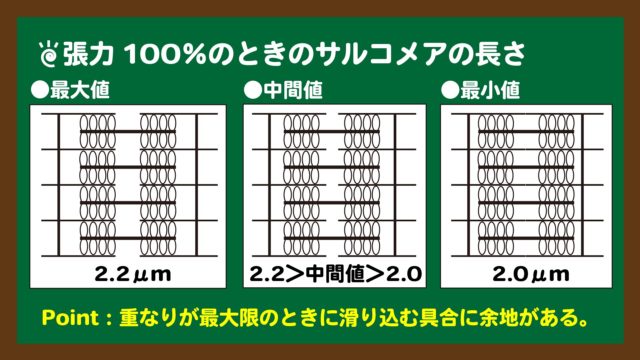スライド８：張力100％のときのサルコメアの長さ

設定文②と図２を読み取ることで、張力が100％のときのサルコメアの長さは2.0～2.2μmであると読み取ることができます。

最後の設定文③は、スライド７中の④の場合に相当します。サルコメアがより短くなってミオシンフィラメントの双方にあるアクチンフィラメントが重なってしまうとずれが生じ、ミオシン頭部とアクチンフィラメントの接地面積が減ることで張力は減少してしまいます。ゆえに、サルコメアの長さ2.0μm未満では、張力が減少しています。

※なお、設定文③にある「抵抗が増して」という表現ですが、アクチンフィラメントどうしが重なった部分に抵抗があると読み取れます。例えが悪いかもしれませんが、手と手を重ねたときに片手を横にスライドさせると抵抗を感じるはずです。

ここまで読み取れたところで、(a)アクチンフィラメントと(b)ミオシンフィラメントの長さを計算しましょう。

計算に使うべき数値は、図２における3.6μmと2.0μmの２つだけです。図２で点を打つ場所は、次のスライド９のようになります。

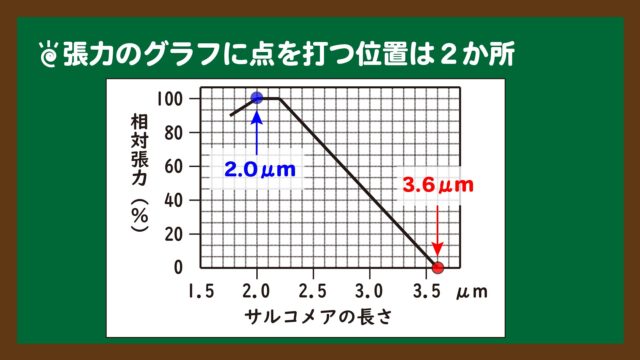スライド９：張力のグラフに点を打つ位置は２か所

この２つの数値は、次のような式を意味しています。

【計算式①】

3.6μm＝ミオシンフィラメントの長さ＋2×アクチンフィラメント半分の長さ

【計算式②】

2.0μm＝2×アクチンフィラメント半分の長さ

式の意味を改めて理解するために、スライド６・８の図をもう一度紹介したものが下のスライド10です。

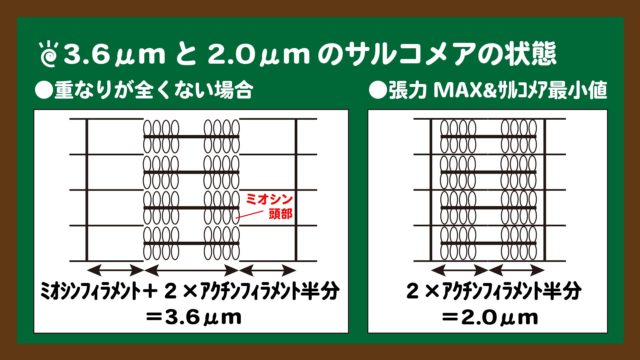スライド10：２つの数値の意味を理解する

※“アクチンフィラメント半分”というところがポイントになります。アクチンフィラメント１本というのは、Z膜を中央にして両側に伸びる繊維のことを指します。

スライド10で理解できたと思いますが、図２における3.6μmと2.0μmというのは、ミオシンフィラメントとアクチンフィラメントの長さを計算できる長さになっています。なので、あとは計算するだけです。

計算すると、次のようになります。

●アクチンフィラメントの長さ→計算式②だけを使う。

2.0μm＝2×アクチンフィラメント半分の長さ

アクチンフィラメントの長さ＝2.0μm

●ミオシンフィラメントの長さ→計算式①にｱｸﾁﾝﾌｨﾗﾒﾝﾄの長さを代入

3.6μm＝ミオシンフィラメントの長さ＋2×アクチンフィラメント半分の長さ

3.6μm＝ミオシンフィラメントの長さ＋アクチンフィラメントの長さ

3.6μm＝ミオシンフィラメントの長さ＋2.0μm

ミオシンフィラメントの長さ＝1.6μm

以上をもとに、(a)アクチンフィラメントの長さは2.0μm、(b)ミオシンフィラメントの長さは1.6μmと計算することができました。

長い説明にうんざりしたと思いますが、次の２つの要点をグラフ中から探せばよいということになります。

ミオシンフィラメントの長さ＋アクチンフィラメントの長さ
アクチンフィラメントの長さ

たったこれだけではありますが、正確に読み取るためにはサルコメアの状態と張力の関係性を図で理解しておくことが必須であると、管理人は感じています。労力はかかりますが、計算式だけを暗記するのではなく、図をイメージできるようになっておきましょう。

補足

数値について

問題をつくるうえで、以下の数値を引用しています。

ミオシンフィラメントの長さ＝1.6μm
アクチンフィラメント半分の長さ＝1.0μm

引用文献：生理学テキスト第７版第２刷、著者：大地陸男、発売年月日：2013年2月15日

バネの張力と筋肉の張力の違い

バネの張力は、引き伸ばした時に、元の形に戻ろうとして生じます。これが、バネの張力です。

対して、筋肉の張力は、収縮したときに、ミオシン頭部とアクチンフィラメントの接触によって生じます。

まとめると、

バネの張力は引き伸ばした時に生じる。
筋肉の張力は収縮した時に生じる。

というように、張力が発生する際の条件が異なっています。

総括

タイトルにある通り、今回は“筋肉の張力のグラフと計算の問題”の解き方を解説しました。いきなり本題となる問題だけでもよかったのですが、解く上で必要となる基本的な知識を問１と問３で確認するようなスタイルに工夫した次第です。問４の最後のPOINTで示しているように公式のようなものを覚えるだけでも幾分は解くことができるかもしれませんが、このテーマを本質的に理解するためには問４解説の序盤から中盤のサルコメアの状態がわかってイメージできるようになることが望ましいと思います。

高校生物は、生物基礎よりもレベルが格段と上がります。管理人の主観では、必要な勉強量は10倍程度になると思っています。医学部や理学部を目指す方は専門に活かすために高校生物を包括的に学んでほしいですが、それ以外の方は高校生物をどのように得点するかという受験戦略が必要になってきます。問４の解説を全部読んで理解した方がいいのか、それとも最後のPOINTだけ見ておくだけに留めるか、そのあたりは自身の目標や力量と相談して決めるとよいでしょう。今回の体験が次の学びにつながると思います。