今回は、「高校生物」の第4章“生殖と発生”に登場する連鎖・組換え価の基本と連鎖の検定交雑の問題の解き方を紹介します。定番の問題をなるべくわかりやすく解説しています。なお、この問題のレベルに到達するには、メンデル遺伝の基礎が必要です。問題を解いてみて全くわからない場合は、まず参考書でメンデル遺伝の基礎を学ぶことをお勧めします。
追記：遺伝の基本レベルの解説記事もつくりました。下の記事は内部リンクをまとめたものになります。
今後、遺伝の法則の用語「優性・劣性」は「顕性・潜性」と言い換えられる予定になっているそうです。入試問題でも言い換えられる可能性が高いので、「顕性・潜性」の表現にも慣れておくとよいでしょう。
演習問題
まずは演習問題として、下のスライド１にある問題を解いてみましょう。標準解答時間は20分です。解けない場合は、すぐに解説を見て解き方を確認しましょう。
スライド１：連鎖・組換え価と検定交雑の問題※問３(1)の問題文にミスがあったため、修正しました。
解き具合はどうだったでしょう。問５までは連鎖と組換え価の基本なので解けたかもしれませんが、問６は難しかったと思います。解答・解説を見て確認してみましょう。
解答
解答は、下のスライド２とスライド３のようになります。
スライド２：連鎖・組換え価と検定交雑の問題の解答１
スライド３：連鎖・組換え価と検定交雑の問題の解答２解説
問１．遺伝子の配置は理解しておこう！
この問題は知識問題です。遺伝子の配置が問われた問題でした。
２つの遺伝子の連鎖or独立のときの配置は、
- 連鎖しているときは、同じ染色体に存在する。
- 独立の関係にある時は、異なる染色体に存在する。
というようになります。あとは、１つの遺伝子、例えばA(a)は、相同染色体の同じ位置に存在することを間違えないようにするだけでした。まとめると、下のスライド４のようになります。
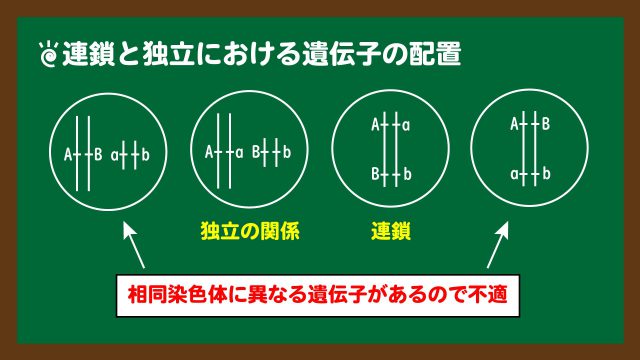スライド４：連鎖と独立における遺伝子の配置問２．連鎖のときは独立の法則とは違う解き方で！
この問題は遺伝の問題です。組換え価の計算の仕方と、完全連鎖の意味が問われた問題でした。
まず(1)についてです。組換え価を使った配偶子の遺伝子型の分離比の求め方は公式があります。その公式を使うと、下のスライド５のようになります。
スライド５：組換え価の公式とその使用例｜AとB（aとb）が連鎖このようにして、組換え価の公式から配偶子の遺伝子型の分離比を求めることができます。ポイントは、
- 組換えが起きた配偶子の遺伝子型は、AbとaBだと読み取る。なぜなら、もとはAB、abが連鎖しているから。
- 組換え価をmとおいて公式を立てている。
- 配偶子の分離比をAB：Ab：aB：ab＝n：m：m：nとしている。
となります。また、公式にはスライド４で表したように２つのパターンがありますが、式を変形しただけです。両方とも覚えておきましょう。
次に(2)についてです。完全連鎖とは、“染色体の乗換えが起きても遺伝子の組み換えが全く起こらない”ことを指します。なので、連鎖している２つの遺伝子には全く組換えが起こらず、配偶子の分離比は染色体の連鎖の状態と変わらないことになります。
スライド４の組換え価の公式ですが、実は万能ではないことに注意が必要です。今回は、AB・abと連鎖しており、組換えで生じる遺伝子型がAb・aBでした。しかし、Ab・aBが連鎖しており、組換えで生じる遺伝子型がAB・abのときは、式を少し立て直す必要があります。その実践が次の問３(1)になるので、併せて確認しましょう！
問３(1)．組換え価の公式を変えることが必要になる！
この問題は遺伝の問題です。問題の内容としては問２と同様で、組換え価を使った演習問題になります。
まず、(1)です。この問題は、問２の注意書きで書いたように、スライド５の公式をそのまま使うことができません。なぜなら、Ab・aBというように連鎖しており、AB・abが組換えで生じるからです。これは、問２(1)とは逆になっています。
このとき、配偶子の分離比を、
- AB：Ab：aB：ab＝n：m：m：n
とおくと、組換え価はnを指すことになります。前述のとおり、AB・abが組換えで生じるからです。なので、スライド５の公式を変形し、下のスライド６のようにします。
スライド６：組換え価の公式とその使用例｜Aとb（aとB）が連鎖こうすると、問題を解くことができます。
混乱を招いたかもしれませんが、ポイントとしては“公式の分子は組換えが起きた方の文字数を置くこと”に注意することです。
ちなみに納得できない場合は、スライド５の公式にm＝12.5を当てはめてみるとよいでしょう。すると、AB：Ab：aB：ab＝7：1：1：7となって誤答になってしまいます。
組換え価の公式は、場合によって変形する必要があることを理解しておこう！
問３(2)、(3)、(4)の簡単な解説
次に(2)ですが、これは、問２(1)と解き方が同じなので、解説は省略させていただきます。
(3)も、問２(2)と意味合いは同じです。組換え価が０％のときは完全連鎖のことを指します。また、スライド５の公式に当てはめると、同じ答えになることがわかるでしょう。
最後の(4)ですが、組換え価が50％のときは２つの遺伝子は独立の関係にあります。公式に代入してみると、AB：Ab：aB：ab＝1：1：1：1となり、独立の法則が成り立つときのAaBbの配偶子の分離比となります。
問４．連鎖で組換えが起こるときの交配！
この問題は遺伝の問題です。連鎖のときの交配を組換え価を使って解く問題でした。
組換えが起こるときの配偶子の遺伝子型の分離比の演習は問２と問３でやったので、交配の部分のみに注目して解説します。解説の図は、下のスライド７です。
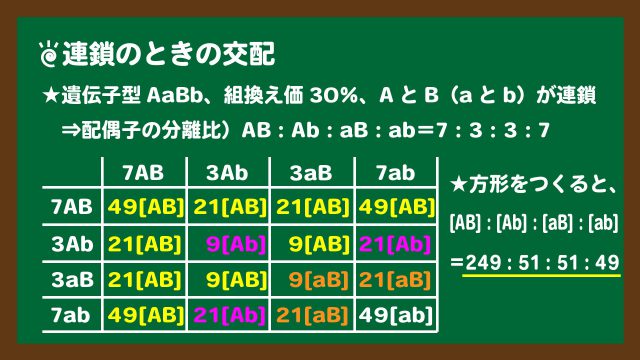スライド７：連鎖で組換えが起こるときの交配の解き方方形の作り方については、二遺伝子雑種の交配と同じです。ただし、配偶子の分離比が異なるので、それぞれの配偶子の遺伝子型に分離比の数を付けています。交配するときは、係数と係数をかけ算して枠の中を埋めていきます。最後にそれぞれの表現型でたし算をして終わりです。
連鎖で組換えが起こるときの交配は、配偶子の遺伝子型の分離比を使って交配表をつくる！
問５．連鎖と検定交雑！
この問題は遺伝の問題です。連鎖で組換えが起こるときの検定交雑の問題でした。
配偶子の分離比を求めますが、じつはF1の分離比がそのまま答えとなります。解き方は二遺伝子雑種の検定交雑のときに紹介したものと同じで、下のスライド８のようになります。
スライド８：連鎖と検定交雑｜配偶子の分離比の求め方こんなかんじで、解き方はシンプルでした。
問６．連立方程式を立てて組換え価を求める！
この問題は遺伝の問題です。まず初見では解けない連鎖と検定交雑の問題でした。
この問題を解くには、文字式を置いて連立方程式を組み立てる必要があります。具体的には、下のスライド９のようなことをします。
スライド９：連鎖と検定交雑｜連立方程式を組む場合改めてこの問題の解き方を解説すると、
- 配偶子の分離比を、AB：Ab：aB：ab＝m：n：n：mと仮定する。
- 交配表をつくる。
- “表現型の文字式の和＝問題文での分離比”なので、表現型４つについて式を立てる。（２つは同じなので、立てる式は実質３つになる。）
- 連立方程式を解くとmとnの数値が出るので、それが配偶子の分離比となる。
というようになります。
ちなみに、ポイントは交配表の一番右下の１つの枠です。ここは、m2＝1なので平方根をつかってm＝1と簡単に導くことができます。また、(2)の問題では、m2＝9なので平方根を使えばm＝3になります。この手の問題では、ここの部分が平方根で簡単な数になるように設定されていることがほとんどです。
このポイントを捉えて連立方程式を解いてみましょう。
★(1)の場合
m2＝1かつ組換価の分離比は正なので、m=1。スライド９の①と②においても『n2＋2nー24＝0』が成り立つ。このnについての連立方程式を解くと、『(n＋6)(nー4)＝0』より『ｎ＝ー6 or 4』となり、組換価は＋なのでｎ＝４となる。
よって、連鎖している配偶子の分離比はAB：Ab：aB：ab＝m：n：n：mと仮定しているので、AB：Ab：aB：ab＝１：４：４：１となる。
★(2)の場合
m2＝9かつ組換価の分離比は正なので、m=3。スライド９の①と②においても『n2＋6nー7＝0』が成り立つ。このnについての連立方程式を解くと、『(n＋7)(nー1)＝0』より『ｎ＝ー7 or 1』となり、組換価は＋なのでｎ＝１となる。
よって、連鎖している配偶子の分離比はAB：Ab：aB：ab＝m：n：n：mと仮定しているので、、AB：Ab：aB：ab＝３：１：１：３となる。
遺伝子型AaBbの表現型の分離比が“よくわからない”かんじになっているときは、配偶子の分離比を文字式で仮定して連立方程式を立てるとよい。
なお連鎖関係については、(1)はAbとaBの連鎖、(2)はABとabの連鎖と言える。
総括
今回の記事では、連鎖の基本から組換え価、さらに発展の検定交雑までを紹介させていただきました。基本をおさえて問６の難易度が高い問題まで、できるようになったでしょうか。解き方が分かった場合でも内容が難しいので、幾度か復習することが望ましいと思います。管理人的には、センター試験あるいは大学入学共通テストでも問６くらいの問題は出題されそうな気がするので、問６は要注意ポイントです。
遺伝の問題のまとめ記事
遺伝の問題について、管理人がつくった問題解説をまとめました。是非ご活用ください。
おわりに
アンケートにご協力ください！
もっとご協力頂けるなら、アンケートページでお答えください。
お役立ちの“まとめ記事”紹介
ページ下でコメントを受け付けております！
下にスクロールすると、コメント欄があります。この記事の質問や間違いの指摘などで、コメントをしてください。管理人を応援するコメントもお待ちしております。なお、返信には時間がかかる場合があります、ご容赦ください。
以上でこの記事は終わりです。ご視聴ありがとうございました。
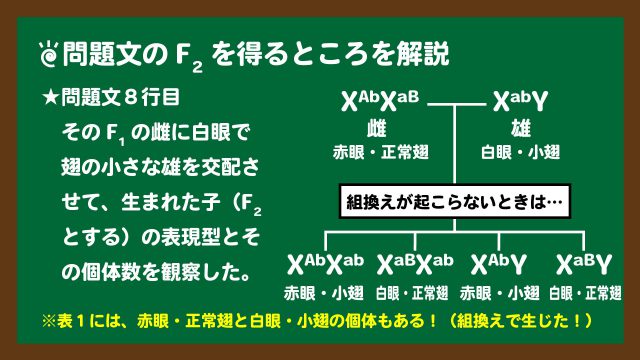
問3(1)のラージBはどこからでてきたのですか？
私がわかってないのかスライドに誤りがあるのか、、ところどころわかんなかったけど、私の苦手なところをピンポイントで解説してくださりとても身になりました！！
バンビ 様
閲覧およびコメントありがとうございます。
ご指摘の通り、問3(1)の問題文にミスがありました。
スライド１を修正して再掲示させていただきました。
ご指摘下さり、誠にありがとうございました。
また微力ながらお役に立つことができ、嬉しい限りです。
今後も高校生物の学び舎をよろしくお願い致します。
管理人シカマルより
こんにちは。
問６の最終的な解答がよくわかりません。
(1)、(2)ともに、それぞれ教えていただきたいです。
よろしくお願いいたします。
み 様
コメント及びご質問ありがとうございます。
ご質問の内容について問６解説に解き方を追記しました。
ポイント枠の前の薄緑の背景色がある部分になります。
連立方程式の計算を示したかたちとなりました。
もし記述の内容がわからない場合は、再度コメントにてご指摘いただけると幸いです。
今後とも高校生物の学び舎をよろしくお願いいたします。
管理人シカマルより。
問６の解説を追記していただいて、ありがとうございます。
理解することができました。
引き続きこちらのサイトで勉強させていただきます。
み 様
再度のコメントありがとうございます。
問題を理解できたようでよかったです。
また、み様のおかげで解説をより充実できたこと嬉しく感じております。
ご質問いただいて誠にありがとうございました。
今後とも高校生物の学び舎をよろしくお願いいたします。
管理人シカマルより。
質問失礼致します。スライド２と３の問2の(1)の答えと問3の(1)について質問があります。
問2の答はAB:Ab:ab:ab＝4:1:1:4とありますがAB:Ab:aB:ab=4:1:1:4ではないでしょうか。問3の答えについても同様で、abが2つあります。スライド５と６では指摘した通りになっているのと僕がやったところの答えがそちらであるため、間違えではないのかどうか確認お願い致します。間違えでなければすいません。
るいと 様
コメント及びご質問ありがとうございます。
ご指摘の通り、画像の内容が誤っておりました。
修正したものをアップロードしました。
この度は当サイトの品質向上にご協力いただきありがとうざいました。
また、返信が遅くなりましたことお詫び申し上げます。
今後とも高校生物の学び舎をよろしくお願いいたします。
管理人シカマルより。