「高校生物」遺伝の問題の解き方|連鎖の伴性遺伝の問題解説(難問)
今回は、「高校生物」の第4章“生殖と発生”に登場する連鎖・組換え価の発展問題である連鎖の伴性遺伝の問題の解き方を紹介します。定番の問題をなるべくわかりやすく解説しています。なお、この問題のレベルに到達するには、メンデル遺伝の基礎が必要です。問題を解いてみて全くわからない場合は、まず参考書でメンデル遺伝の基礎を学ぶことをお勧めします。
追記:遺伝の基本レベルの解説記事もつくりました。下の記事は遺伝の問題の内部リンクをまとめたものになります。

今後、遺伝の法則の用語「優性・劣性」は「顕性・潜性」と言い換えられる予定になっているそうです。入試問題でも言い換えられる可能性が高いので、「顕性・潜性」の表現にも慣れておくとよいでしょう。
演習問題
まずは演習問題として、下のスライド1にある問題を解いてみましょう。標準解答時間は20分です。解けない場合は、すぐに解説を見て解き方を確認しましょう。
解き具合はどうだったでしょう。難関大学レベルの問題なので、かなり難しかったと思います。解けた方も解けなかった方も、解答解説を見て確認してみましょう。
解答
問1.33.5%
問2.⑤
解説
問1.連鎖の伴性遺伝で組換え価を求める難問!
この問題は遺伝の問題です。2遺伝子が性染色体上で連鎖している伴性遺伝で組換え価を求めるという、かなり難易度の高い問題でした。
問題文を読むと、形質がアルファベットで指定されていないので、まずは自分で指定するところから始めます。ここでは仮に、
- 赤眼:A、白眼:a
- 正常翅:B、小翅:b
とします。また、“伴性遺伝なのに雌・雄両方で遺伝子が発現すること”、“キイロショウジョウバエの性染色体はXY型(雌:XX、雄:XY)”であることから、
- 遺伝子A(a)、B(b)は、X染色体上に存在する。
と判断します。
では、問題文に沿って、図をつくっていきましょう。
まずは、問題文7行目の“F1を得た”からです。これは、下のスライド2のようになります。なお、雌の2つのX染色体上の遺伝子は、純系なので同じものになります。
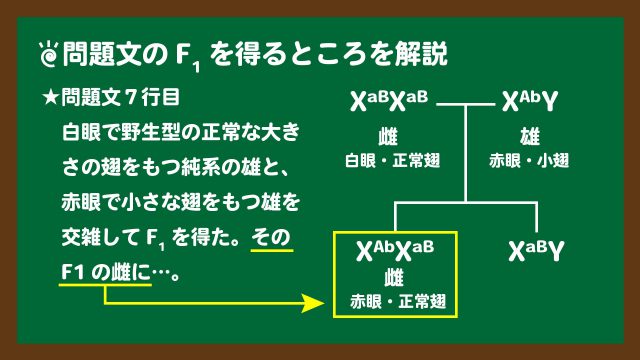 スライド2:問題文7行目のF1を得るところを図説
スライド2:問題文7行目のF1を得るところを図説このようにして、目的のF1の雌を導くことができました。
次に、問題文9行目の“F2”を得るところです。これは、下のスライド3のようになります。左は問題文、右は交配の図です。
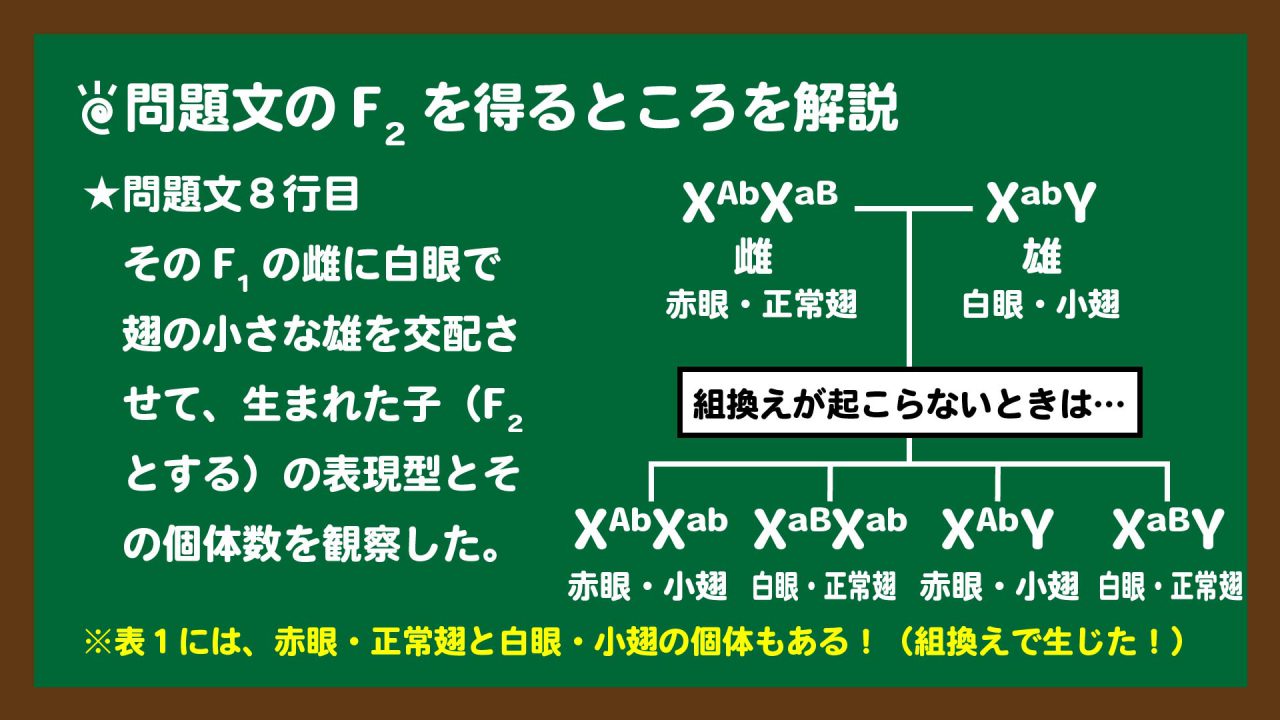
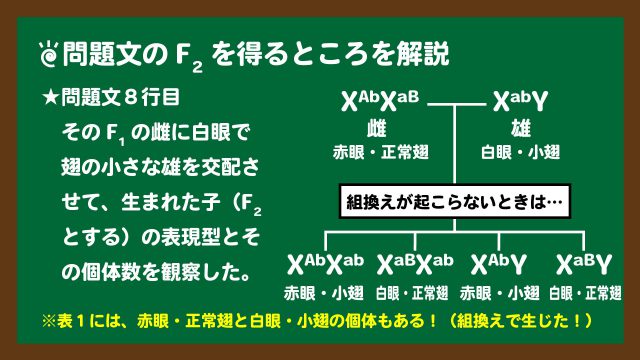 スライド3:問題文のF2を得るところを図説
スライド3:問題文のF2を得るところを図説仮に組換えが起こらないとすると、赤眼・小翅と白眼・正常翅しか生まれないことがわかります。しかし、表1には、赤眼・正常翅と白眼・小翅の個体もあります。よって、赤眼・正常翅(XAB)と白眼・小翅(Xab)の個体は組換えによって生じたと判断することができます。そうすると、指定されているF1の雌の配偶子の分離比は、表1の個体数をそのまま使って、
- XAB:XAb:XaB:Xab=114:202:226:102
とおくことができます。(なお、数値をそのまま使えるのは、交配相手が劣性遺伝子しか持たないためです。)
あとはこの分離比をもとに、組換え価を求めます。その計算は、下のスライド4のようになります。
 スライド4:組換え価の公式を使って組換え価を求める
スライド4:組換え価の公式を使って組換え価を求めるこのようにして、解答となる組換え価を求めることができました。
問1のポイントは、F2を導くときに一旦組換えが起こらないと仮定してみること。そうすると、表1を見て組換えが起きた形質がわかる!
問2.組換え価×合計で、組換えの起きた個体数を求める!
この問題は遺伝の問題です。問1で求めた組換え価を使って交配結果の個体数を導き、選択肢を選ぶ問題でした。
ここでも問2の問題文にならって図説していきたいと思います。まず、問2のF1を得るところまでは、下のスライド5のようになります。
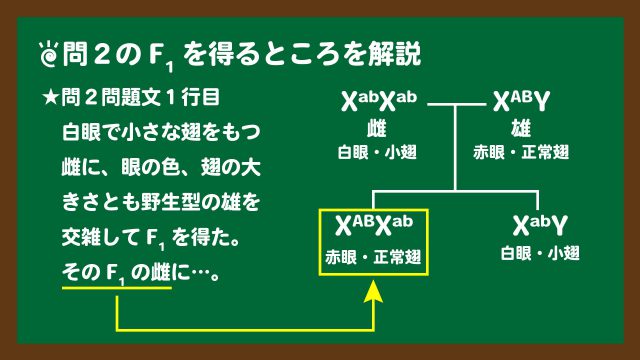 スライド5:問2のF1を得るところを図説
スライド5:問2のF1を得るところを図説このようにして、目的のF1の雌を導くことができました。
さらにこのF1に、問題文に沿って交配を行います。この部分は、下のスライド6のようになります。右図の交配では、仮に組換えが起こらないとした場合の交配結果になります。
 スライド6:問2のF1を交配させるところを解説
スライド6:問2のF1を交配させるところを解説問1と同じように、仮に組換えが起こらないと仮定すると、赤眼・正常翅と白眼・小翅しか出現しません。しかし、表2を見ると、どの選択肢でも赤眼・小翅と白眼・正常翅の個体も存在します。つまり、赤眼・小翅と白眼・正常翅の個体は組換えによって生じたと判断することができます。
組換えによって生じた表現型が赤眼・小翅と白眼・正常翅だとわかったところで、あとは個体数を推定する作業を行います。この作業は至って簡単で、
- 個体の合計数×組換え価=組換えが起きた個体数
なので、計算を行うのみです。すると、組換えが起きた個体数は、
- 1130×33.5÷100≒378
- 1247×33.5÷100≒417
- 1310×33.5÷100≒438
- 1410×33.5÷100≒472
- 1304×33.5÷100≒436
となります。あとは、“赤眼・小翅の個体数+白眼・正常翅の個体数”とほぼ一致する選択肢を選ぶだけになります。よって、⑤が正答でした。
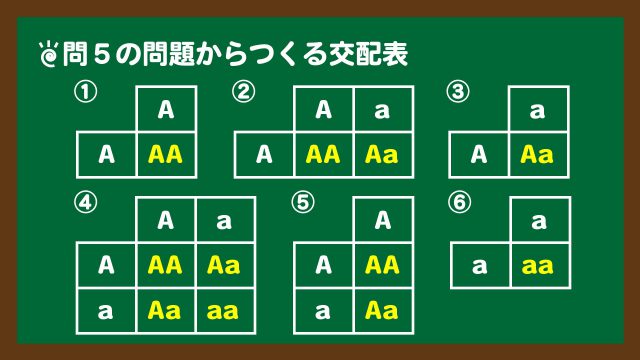
ちなみに、①~⑤の選択肢のすべてを計算しなければならないわけではありません。①と③は組換えが起きた個体が違うので選択肢から外れますし、④は分離比がほぼ1:1:1:1なので独立、つまり組換えが起きていないので、これも選択肢から外れます。計算すればよいのは②と⑤のみでした。
総括
この問題も一見難しいように見えますが、解説を見ると割とスムーズに解くことができることを理解していただけたと思います。ただし、難易度的には連鎖の総仕上げレベルです。以下のまとめ記事にもう1つ総仕上げの問題の内部リンクを貼っていますので、そちらも併せて勉強するとよいと思います。
ここまでできるようになったら、連鎖の問題はほぼできるようになったと思ってもらって大丈夫です。理系の方はさらに、キメラマウスや集団遺伝などを学ぶとよいでしょう。
遺伝の問題のまとめ記事
遺伝の問題について、管理人がつくった問題解説をまとめました。是非ご活用ください。

おわりに
アンケートにご協力ください!
もっとご協力頂けるなら、アンケートページでお答えください。

お役立ちの“まとめ記事”紹介




以上でこの記事は終わりです。ご視聴ありがとうございました。